11. NODAĻA

INDUKCIJAS IZMANTOŠANA ALGORITMU PAREIZĪBAS PIERĀDĪŠANĀ

(INDUKCIJAS METODES PIELIETOJUMI)

Lielāko daļu līdz šim aplūkoto piemēru un uzdevumu var iedalīt vienā no trim grupām:

1. uzdevumi, kuros jāpierāda kāda apgalvojuma (vienādības, nevienādības, viena skaitļa daīšanas ar otru skaitli) patiesums;
2. uzdevumi, kuros jākonstruē kāds objekts vai objektu virkne (36. piemērs, 56. piemērs, 59. piemērs utt.);
3. uzdevumi, kuros jāizstrādā metode (algoritms) veselas uzdevumu klases risināšanai (piemēram, 35. piemērs par laupījuma sadalīšanu un 5. nodaļā apskatītais skaitļu reizināšanas algoritms).

Iepriekš apskatītie c) tipa piemēri bija tādi, kuros indukcija galvenokārt tika izmantota pašu algoritmu aprakstīšanai; aprakstīto algoritmu pareizība pēc to konstrukcijas bija acīmredzama.

Šajā nodaļā mēs apskatīsim piemērus, kuros indukcija galvenokārt tiek izmantota, pierādot aprakstīto algoritmu pareizību.

85. piemērs. Konfekšu kaudzītē ir n konfektes. Divi spēlētāji A un B pēc kārtas izdara pa vienam gājienam; pirmo gājienu izdara spēlētājs A. Ar vienu gājienu katra kaudzīte, kurā ir vairāk nekā viena konfekte, jāsadala divās mazākās kaudzītēs, kas katra sastāv no vesela skaita (varbūt vienas pašas) konfekšu. Zaudē tas spēlētājs, kurš nevar izdarīt gājienu. Kādām n vērtībām A var uzvarēt? Kā jāspēlē, lai uzvarētu?

Pierādīsim šādu teorēmu.

I teorēma. Ja n2^k-1, tad spēlētājs A var uzvarēt. Lai uzvarētu, viņam katrā savā gājienā jāsadala kaudzītes tā, lai vislielākajā kaudzītē konfekšu skaits būtu 2^l-1.

Ja n=2^k-1, tad pareizi spēlējot, var uzvarēt spēlētājs B (k un l- naturāli skaitļi).

Definēsim spēles stāvokļa jēdzienu. Ja uz galda atrodas m kaudzītes konfekšu, kas satur attiecīgi k₁, k₂, …, k_m konfektes, tad sacīsim, ka spēle atrodas stāvoklī <k₁, k₂, …, k_m>, turklāt pieņemsim, ka k₁ nav mazāks kā katrs no skaitļiem k₂, …, k_m.

Acīmredzot sākumā spēle atrodas stāvoklī <n>. Uzvar tas spēlētājs, pēc kura gājiena spēles stāvoklis ir <1; 1;…; 1>, jo tad visas kaudzītes satur pa vienai konfektei un pretiniekam nav iespējams izdarīt gājienu.

Pierādīsim vispārīgāku teorēmu.

II teorēma. Spēlētājs, kuram jāizdara gājiens, kad spēle ir stāvoklī <k₁; k₂; …; k_m>, var uzvarēt ja k₁₂^l-1, lN. Lai uzvarētu, viņam spēle jānoved (un viņš to var izdarīt) stāvoklī <k^'₁; k^'₂;…; k^'_m¹>, kur k^'₁=2^l-1, lN; spēlētājs, kam jāizdara gājiens, kad spēle ir stāvoklī <k₁; k₂; …; k_m>, kur k₁=2^l-1, lN, nevar uzvarēt, ja pretinieks spēlē pareizi.

Pielietojot šo teorēmu spēlei, kas ir stāvoklī <n>, iegūstam I teorēmu (m=1, k₁=n).

Pierādīsim II teorēmu ar indukciju pēc k₁.

Bāze. Ja k₁=1, tad k₁=k₂=…=k_m=1, spēlētājs A nevar izdarīt gājienu un tātad zaudē. Tas saskan ar teorēmas apgalvojumu, jo k₁=1=2₁-1.

Ja k₁=2, tad dažās kaudzītēs ir 2 konfektes, bet dažās citās (ja tādas ir)- tikai viena konfekte. Spēlētājs A var uzvarēt, sadalot katru kaudzīti, kurā ir 2 konfektes, divās kaudzītēs pa vienai konfektei katrā. Tas saskan ar teorēmas apgalvojumu, jo 22^l-1, lN, un pēc spēlētāja A gājiena konfekšu skaits lielākajā kaudzītē ir 2¹-1.

Pāreja "<nn", ja n3. Pieņemsim, ka teorēma jau pierādīta, ja k₁=1, k₁=2…, k₁=n-1. Pierādīsim to, ka ja k₁=n. Šķirosim divus gadījumus.

1. n=2^l-1, lN, l>1. Ar savu gājienu spēlētājam A jāsadala divās daļas arī tā kaudzīte, kurā ir k₁ konfektes. Vismaz vienā no iegūtajām divām kaudzītēm būs ne mazāk kā konfektes. Tātad pēc spēlētāja A gājiena vislielākajā kaudzītē konfekšu skaits būs lielāks nekā 2^l-1-1, bet mazāks nekā 2^l-1, jo pirms pēdējās dalīšanas nevienā kaudzītē nebija vairāk kā 2^l-1 konfektes, un katrā kaudzītē ar vairāk nekā vienu konfekti pēc spēlētāja A gājiena to skaits samazinājās. Tātad pēc spēlētāja A gājiena spēles stāvoklis ir <k^'₁; k^'₂;…; k^'_m1>, kur k^'₁=2^l-1-1<k^'₁<2^l-1, t.i., k^'₁₂^ss, sN. Tā kā k^'₁<n, tad pēc induktīvā pieņēmuma spēlētājs, kuram šjā stāvoklī jāizdara gājiens, t.i., spēlētājs B, var uzvarēt, ko arī vajadzēja pierādīt; spēlētājs A zaudēs, ja B spēlēs pareizi
2. n2^l-1, lN. Pierādīsim, ka spēlētājs A var novest spēli stāvoklī <k^'₁; k^'₂;…; k^'_m1>, kur k'₁<n un k'₁=2^l-1, lN; tad pēc induktīvā pieņēmuma spēlētājs B, kuram šajā jaunajā stāvoklī jāizdara gājiens, nevar uzvarēt, ja A spēlē pareizi, un induktīvā pāreja būs izdarīa arī šajā gadījumā.

Ja n=k₁₂^l-1, lN tad eksistē tāds naturāls skaitlis s, ka 2^s-1<k₁<2^s+1-2. Katru kaudzīti, kurā vairāk nekā 2^s-1 konfektes (tātad arī kaudzīti, kurā ir k₁ konfektes), sadalīsim divās daļās tā, lai vienā daļā būtu 2^s-1 konfektes, bet otrā daļā- visas pārējās. Skaidrs, ka neradīsies neviena kaudzīte, kurā ir vairāk nekā 2^s-1 konfektes, bet vismaz vienā kaudzītē būs 2^s-1 konfektes. Nav svarīgi, kā sadala pārējās kaudzītes: pēc dalīšanas notām iegūsim kaudzītes, kurās katrā ir mazāk 2^s-1 konfektes.

Induktīvā pāreja pierādīta.

Aplūkoto risinājumu varēja formulēt arī šādi.

Sadalīsim visus spēles stāvokļus <k₁; k₂;…; k_m> divās grupās U un Z. Grupa U sastāv no visiem tiem stāvokļiem, kuriem k₁=2^l-1 lN. Ievērosim, ka

1. stāvoklis < 1; 1; …; 1>, pēc kura vairs nevar izdarīt gājienu, ietilpst grupā Z;
2. no katra stāvokļa, kas ietilpst grupā U, var pāriet uz kādu no stāvokļiem. Kas ietilpst grupa Z;
3. no katra stāvokļa, kas ietilpst grupā Z, var pāriet tikai uz stāvokļiem, kas ietilpst grupā U.

Induktīvajā pārejā jau pierādījām, ka pēdējie divi apgalvojumi ir patiesi.

No šejienes izriet, ka spēlētājs, kuram jāizdara gājiens brīdī, kad spēles stāvoklis ietilpst grupā U, ir uzvarējis, bet spēlētājs, kuram jāizdara gājiens brīdī, kad spēles stāvoklis pieder pie grupas Z ir zaudējis. Tiešām, ja spēlētājam A jāizdara gājiens brīdī, kad spēles stāvolkis pieder pie U, viņš var novest spēli stāvoklī, kas ietilpst zrupā Z; tad pretiniekam ar savu gājienu (ja viņš to var izdarīt) noteikti jāatgriežas kādā stāvoklī no U. Līdz ar to A vienmēr jāizdara gājiens tikai brīžos, kad spēles stāvoklis pieder pie U; tā kā <1; 1;…,1> Z, tad A vienmēr varēs izdarīt gājienus; gājienu pietrūks spēlētājam B. Ja spēlētājam A jāizdara gājiens brīdī, kad spēles stāvoklis pieder pie Z, tad B saņem gājienu, kad spēles stāvoklis pieder pie U un tad B pēc pierādītā var uzvarēt.

86. piemērs. Aprakstīsim algoritmu kvadrātsaknes vilkšanai no naturāliem skaitļiem un pierādīsim tā pareizību.

A l g o r i t m a a p r a k s t s. Vispirms tā naturālā skaitļa pieraksta cipari, no kuriem jāvelk kvadrātsakne, jāsadala grupās pa divi, sākot no beigām. (Līdz ar to ciparu grupā skaitļa sākumā būs vai nu viens, vai divi cipari.) Pieņemsim, ka izveidojušās k grupas. Naturālos skaitļus, kuru pieraksts ir izveidotās ciparu grupas, apzīmēsim, sākot no kreisās puses, ar s₁, s₂, …, s_k; s₁ ir vai nu viencipara vai divciparu skaitlis, bet s₂, …, s_k ir divciparu skaitļi. Algoritma darbības rezultātā iegūsim k ciparu skaitli, pie tam tā cipari tiks iegūti secīgi no kreisās uz labo pusi; apzīmēsim šos pagaidām nezināmos ciparus ar c₁, c₂, …, c_k.

Aprakstīsim to iegūšanu ar algoritmu induktīvi.

Bāze. Apskatīsim skaitli s₁. Par c₁ izvēlēsimies lielāko ciparu, kura kvadrāts nepārsniedz s₁; par atlikumu A₁ nosauksim starpību

A₁=s₁-c²₁.

Pāreja ii+1, ja I<k. Pieņemsim, ka, izmantojot skaitļus s₁, s₂, …, s_i, iegūti cipari c₁, c₂, …, un atlikums ir A_i.

Pierakstīsim atlikumam A_i labajā pusē skaitli s_i+1; iegūsim skaitli ;. Pareizināsim skaitli ar 2 un iegūto reizinājumu apzīmēsim ar D_i+1. Par ciparu c_i+1 jāņem maksimālais cipars x, kas apmierina īpašību: pierakstot ciparu x skaitlim D_i+1 labajā pusē un skaitli reizinot ar x, reizinājums nepārsniedz

Atlikumu A_i+1 aprēķina pēc formulas

.

Kad visas ciparu grupas (to skaits ir k) apstrādātas un iegūti k cipari, jāpārbauda, vai A_k=0. Ja A_k=0, tad skaitļa kvadrāts vienāds ar doto skaitli un tātad . Ja A_{k0, tad no dotā skaitļa kvadrātsakni naturālos skaitļos izvilkt nevar.}

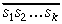
Ilustrēsim algoritma darbību ar diviem piemēriem.

87. piemērs. Atrast .

Sadalām zemsaknes skaitļa ciparus grupās tā, kā norādīts algoritma aprakstā:

.

Tā kā s₁=1, tad c₁=1 un A₁=s₁-c₁²=1-1=0. Pierakstām to šādi

.

Pierakstot atlikumam A₁=0 labajā pusē ciparu grupu s₂=44, iegūstam skaitli 044. Attēlojam to kā ciparu grupas s₂ "nonešanu uz leju":

Reizinot skaitli c₁=1 ar 2, iegūstam D₂=c_{12=2. Pierakstām} D₂ pa kreisi no skaitļa 044, atdalot tos ar vertikālu svītru:

Lielākais cipars x, ko var pierakstīt skaitlim D₂=2 labajā pusē tā, lai būtu , ir 2. Cipara 2 pierakstīšanu skaitļa D₂=2 labajā pusē un tai sekojošo skaitļa reizināšanu ar 2 izdarām pa kreisi no vertikālās svītras, bet rezultātu R₂=222 pierakstām zem skaitļa :

Tātad c₂=2 un . Ciparu c₂=2 rakstām aiz cipara c₁=1, bet A₂- zem pēdējās horizontālās svītras:

Pēc tam atrodam , D₃=122=24. Iegūstam

Lielākais cipars x, ko var pierakstīt labajā pusē skaitlim D₃=24 tā, lai būtu , ir 0. Tāpēc c₃=0, R₃=2400=0, . Iegūstam

Tālāk atrodam , D₄=1202=240 un, rīkojoties kā iepriekš, iegūstam

Visas četras ciparu grupas apstrādātas, un atlikums A₄=0. Tāpēc.

88. piemērs. Atrast

Saskaņā ar algoritmu iegūstam

Visas trīs ciparu grupas apstrādātas, bet atlikums A_{30. Tāpēc nav naturāls skaitlis.}

Pārbaudīsim, vai abos apskatītajos piemēros esam ieguvuši pareizu rezultātu.

Nav grūti pārliecināties, ka 1202²=1444804.

Tātad 87. piemērā ar aplūkoto algoritmu ir iegūts pareizs rezultāts. Tāpat nav grūti pārliecināties, ka 399²=159201 un 400²= 160 000, tātad

Tā kā 159636 atrodas starp divu naturālu kaimiņu skaitļu kvadrātiem, tad tas nav naturāla skaitļa kvadrāts. Tātad arī 88. piemērā ar aplūkoto algoritmu iegūtais rezultāts ir pareizs.

Kāda situācija izveidojusies?

Esam aprakstījuši algoritmu, kuru var pielietot jebkuram naturālam skaitlim. Skaidrs, ka veicamo darbību skaits katram naturālam skaitlim ir galīgs, jo jāapstrādā visas ciparu grupas, bet to skaits ir galīgs. Mēs arī apgalvojām, ka ar algoritmu iegūtais skaitlis ir kvadrātsakne no dotā skaitļa, ja pēdējais atlikums ir 0; ja pēdējais atlikums nav 0, tad no dotā skaitļa kvadrātsakni naturālos skaitļos izvilkt nevar. Esam arī pierādījuši, ka šis apgalvojums ir patiess divos atsevišķos gadījumos.

Vai teiktais nozīmē, ka šis apgalvojums ir patiess arī visos citos gadījumos, t.i., ka, rīkojoties aprakstītajā veidā par katru naturālu skaitli var noskaidrot, vai tam eksistē naturāla kvadrātsakne vai ne, un, ja eksistē, tad to var atrast? Protams, ka, nē! No tā, ka vispārīgs apgalvojums ir patiess vairākos atsevišķos gadījumos, nevar secināt, ka tas ir patiess vienmēr - arī citos gadījumos.

Pierādīsim, ka ar aplūkoto algoritmu par katru naturālu skaitli var noskaidrot, vai šim skaitlim eksistē vai neeksistē naturāla kvadrātsakne; ja šāda kvadrātsakne eksistē, tad, izmantojot algoritmu, to var aprēķināt. Pierādīsim vispārīgāku teorēmu; vajadzīgais apgalvojums būs tā secinājums.

6. teorēma. Skaitlis , ko iegūst no skaitļa (s₁, s₂,… s_k- no dotā skaitļa izveidotās ciparu grupas) ar aplūkoto algoritmu pēc pirmo n skaitļu s₁, s₂, …, s_n apstrādes, ir lielākais naturālais skaitlis, kura kvadrāts nepārsniedz skaitli , bet atlikuma A_n var aprēķināt pēc formulas

.

Iedomāsimies uz brīdi, ka teorēma pierādīta. Ja n=k, iegūsim šādu secinājumu. Kad skaitļa apstrāde ar aplūkoto algoritmu pabeigta, tad skaitlis ir lielākais naturālais skaitlis, kura kvadrāts nepārsniedz M, bet atlikums . Tāpēc, ja ja A_k=0, tad , tātad ir aprēķināta kvadrātsakne no skaitļa M. Ja turpretī A_{k0, tad ievērojot, ka} a_{k0, iegūstam nevienādību} A_k>0; Tātad . Tā kā ir l i e l ā k a i s naturālais skaitlis, kura kvadrāts nepārsniedz M, tad t.i., m atrodas starp divu naturālu kaimiņu skaitļu un kvadrātiem, t.i., m nav naturāla skaitļa kvadrāts, ko arī vajadzēja pierādīt. Tātad no 6. teorēmas tiešām izriet aplūkotā algoritma pareizība.

Atliek pierādīt 6. teorēmu.

6. teorēmas pierādījums ideju ziņā ir vienkāršs, bet tehniski sarežģīts, tāpēc tā izpratnē var rasties grūtības. Tomēr ieteicam lasītājam censties to apgūt. Matemātikā iespējamas divu veidu grūtības: principiālas, kas saistītas ar jaunu ideju izvirzīšanu un uztveršanu, un tehniskas, kas saistītas ar šo ideju realizēšanu. Radošam darbam matemātikā galvenokārt nepieciešamas spējas pārvarēt pirmā veida grūtības; bet, lai šīs spējas varētu pilnā mērā izpausties, nepieciešams virtuozi pārvaldīt dažādus tehniskus paņēmienus, spēt viegli pārvarēt nebūtiskus šķēršļus, lai varētu koncentrēt uzmanību un spēkus galveno uzdevumu veikšanai. Raugoties no šāda viedokļa, turpmāk aplūkoto pierādījumu var salīdzināt ar sarežģītu pirkstu vingrinājumu, gammu un akordu sēriju pianista apmācības procesā, un šī pierādījuma izparatne liecina par diezgan augstu lasītāja matemātisko kultūru.

Kā būtu visdabiskāk pierādīt 6. teorēmu? Šī teorēma runā par stāvokļiem, kādi rodas algoritma izpildes procesā, apstrādājot vispirms vienu, pēc tam otru, …, n-to, …ciparu grupu. Tāpēc pats dabīgākais ceļš- izdarīt indukciju pēc ciparu grupu skaita n.

Bāze. Ja n=k, teorēmā izteiktais apgalvojums ir patiess; tas tieši izriet no algoritma bāzes apraksta.

Pāreja nn+1, ja n<k. Pieņemsim, ka teorēmas apgalvojums ir patiess, ja skaitļa apstrādāto grupu skaits ir n. Tas nozīmē, ka pēc ciparu grupu s₁, s₂, …, s_n apstrādes

1. iegūtais skaitlis ir lielākais naturālais skaitlis, kura kvadrāts nepārsniedz , t.i.,

(1)

un

(2)

1. atlikums A_n apmierina vienādību

.

(3)

Nevienādība (2) seko no tā, ka ir lielākais naturālais skaitlis, kura kvadrāts nepārsniedz , t.i., jau nālošā naturālā skaitļa kvadrāts pārsniedz .

Pēc tam saskaņā ar algoritmu aprēķina skaitli

(4)

un atrod vislielāko no tiem cipariem x, kas apmierina nevienādību

(5)

Vislielāko ciparu x, kas apmierina nevienādību (5), izvēlas par c_n+1.

Atradīsim nevienādības, kas raksturo ciparu c_n+1. Tā kā c_n+1 apmierina nevienādību (5), tad

Rn+1=(10Dn+1+cn+1)cn+1<100An+sn+1.

(6)

Ja c_n+1+1 ir cipars, tad c_n+1+1 neapmierina vienādību (5), jo c_n+1- lielākai no cipariem x, kas apmierina (5); tad pareiza ir nevienādība

(10Dn+1+cn+1+1)(cn+1+1)>100An+sn+1

(7)

Pierādīsim, ka nevienādība (7) pareiza tarī tad, ja c_n+1+1=10, t.i.,

(10Dn+1+10)10>100An+sn+1.

(8)

No sakarībām (3), (4) un (8 ) iegūstam nevienādībai (8) ekvivalentu nevienādību

(9)

jeb

(10)

Izmantojot nevienādību (2), secinām, ka nevienādības (10) kreisajā pusē atrodas skaitlis, kas nav mazāks par 100. Tā kā s_n+1 ir divciparu skaitlis, tad nevienādība (10) pierādīta.

Tātad nevienādība (7) pareiza visām iespējamām c_n+1 vērtībām.

Lai izdarītu induktīvo pāreju, jāpierāda, ka

1. ir lielākais naturālais skaitlis, kura kvadrāts nepārsniedz ;
2. atlikums A_n+1, ko saņēmām pēc formulas

,

(11)

apmierina vienādību

(12)

Pierādīsim vispirms vienādību (12). Tiešām,

(pārveidojumos izmantotas vienādības (3), (4) un (11) un R_n+1 definīcija).

Acīmredzot pierādāmo apgalvojumu a) var izteikt ar šādām divām nevienādībām

(13)

un

(14)

Pārbaudīsim vai nevienādība (13) ir pareiza:

ko arī vajadzēja pierādīt (pārvietojumos izmantotas sakarības (4), (6) un (3)).

Pārbaudīsim vienādību (14)

ko arī vajadzēja pierādīt (pārveidojumos izmantotas sakarības (7) un (3)).

Induktīvā pāreja un līdz ar to arī 6. teorēma pierādīta.

50. zīmējumā attēlota 6. teorēmas induktīvās pārejas loģiskā shēma.

Atzīmēsim, ka abos šajā nodaļā aplūkotajos piemēros tika pierādīts spēcīgāks apgalvojums nekā tas, kas nepieciešams algoritma pareizības konstatēšanai. Tā otrajā piemērā pierādījām arī apgalvojuma par atlikumu A_n vērtībām, t.i., izmantojām metodi, kas tika aplūkota 6. nodaļā.

50. zīm.

Uzdevumi paškontrolei XI

171. Akmeņu kaudzē ir n akmeņu. Divi spēlētāji pēc kārtas ņem no tās akmeņus. Spēlētājs, kurš izdara pirmo gājienu, nedrīkst pirmajā gājienā paņemt visus akmeņus; katrā tālākajā gājienā drīkst paņemt ne vairāk akmeņu, kā iepriekšējā gājienā paņēmis pretinieks. Uzvar tas, kurš paņem pēdējo akmeni. Kā jāspēlē, lai uzvarētu?

172. Analizēt iepriekšējo spēli, ja otrais nosacījums aizstāts ar šādu: katrā no tālākajiem gājieniem drīkst paņemt ne vairāk kā dubultotu akmeņu skaitu, kurus iepriekšējā gājienā paņēmis pretinieks.

173. Akmeņu kaudzē n akmeņu. Divi spēlētāji pēc k; kārtas ņem no tās akmeņus. Visus kaudzē palikušos akmeņus drīkst paņemt tikai tad, ja akmeņu skaits kaudzē nepārsniedz iepriekšējā gājienā pretinieka paņemto akmeņu skaitu; citādu ierobežojumu nav. Uzvar tas, kurš paņem pēdējo akmeni. Kā jāspēlē, lai uzvarētu?

174. Spēlētāja A rīcībā ir 1 km garš taisnes nogrieznis - "banka". Spēlētājs drīkst dot spēlētājam A glabāšanā dažādus mazus taisnes nogrieznīšus, ievērojot šādus nosacījumus:

a) nogriežņus var nodot glabāšanā un pieprasīt atpakaļ jebkurā laikā un jebkurā kārtībā;

b) katrs glabāšanā nodotais taisnes nogrieznis jānovieto uz 1 km garā nogriežņa , un to nedrīkst pārvietot līdz brīdim, kad spēlētājs B to pieprasa atpakaļ;

c) nekādiem diviem taisnes nogrieznīšiem, kas novietoti uz nogriežņa un vēl nav pieprasīti atpakaļ, nedrīkst būt kopēju punktu;

d) katrā laika momentā spēlētājs B zina, kurā vietā uz nogriežņa novietots katrs glabāšanā nodotais uzgrieznītis;

e) nevienā laika momentā glabāšanā nodoto nogrieznīšu garumu summa nepārsniedz 1 mm.

Pierādīt, ka spēlētājs B var nodot spēlētājam A glabāšanā nogriežņus un pieprasīt tos atpakaļ tādā kārtībā, ka spēlētājs A pēc galīga soļu skaita nevarēs uz nogriežņa novietot pusmilimetru garu nogriezni.

175. Dotas 2ⁿ-1 dažādas masas monētas. Mēs zinām, kura monēta smagākā, kura- otrā smagākā utt. Bez tam mūsu rīcībā ir sviras svari bez atsvariem un vēl viena monēta, par kuras masu ir zināms tikai, ka tā atšķiras no visu pārējo monētu masām. Pierādīt, ka ar n svēršanām iespējams noteikt, par kurām no dotajām monētām šī 2ⁿ-tā monēta ir vieglāka, bet par kurām- smagāka.

176. Dotas n dažādas masas monētas un sviras svari ar atsvariem. Pierādīt, ka ar n[log₂n] svēršanām iespējams sakārtot monētas masu augšanas secībā..

178. Pieņemsim, ka, pastāvot 176. uzdevuma nosacījumiem, mums jāatrod tikai viena pati k-tā smagākā monēta (k=1, 2, …, n). Pierādīt, ka to var izdarīt, izmantojot ne vairāk kā 15n-163 svēršanas, ja n>32.

*178. Pierādīt, ka naturālos skaitļus no 1 līdz var sadalīt n grupās tā, ka nekādu divu vienas grupas skaitļu starpība nepieder pie šīs grupas.

ĪSS LITERATŪRAS APSKATS.

Matemātiskām spēlēm veltīta ļoti plaša literatūra (sk., piemēram, [35], [40] un tur norādītos darbus); tomēr pierādījumi parasti nav tik stingri, kā tas darīts 85. piemērā. Ieteicam lasītājam katru spēli, ko viņam izdodas izanalizēt "intuitīvi", aprakstīt arī precīzi, izmantojot matemātisko indukciju.

Par jautājumiem, kas saistīti ar algoritmu un programmu pareizības pierādīšanu, sk., piemēram [11], 42.-45. Un 48. lpp., [49], 362.-365., 372., 388. lpp.

175.-177. uzdevumi saistīti ar informācojas kārtošanas problēmām, kurām mūsdienu skaitļošanas tehnikas izmantošanā ir ārkārtīgi svarīga nozīme. Labākā grāmata, kurā ir arī daudz uzdevumu, ir [50].

Indukcijas pielietojums dažādu shēmu konstruēšanā un to pareizības pierādījumos var atrast rakstos [51] un [52].

178. uzdevumu var vispārināt šādi: kāds ir maksimālais skaitlis f(n), kuram visus naturālos skaitļus no 1 līdz f(n) var sadalīt grupās tā, ka nekādu divu vienas grupas skaitļu starpība nav no šīs pašas grupas? 178. uzdevumā risinājums parāda, ka ; bez tam, pierādīts, ka

.

Zināmas ir tikai šādas f(n) vērtības: f(1)=1, f(2)=4, f(3)=13, f(4)=44; nedaudz uzlabot 178. uzdevumā doto apakšējo novērtējumu palīdz nevienādība

Piemēram, par f(5) zināms, ka 133f(5)327. Jebkāds progress f(n) vērtību atrašanā vai robežu precizēšanā būtu ievērojams matemātisks sasniegums.